第二节 u检验
u检验(亦称T检验),它根据正态分布规律作假设检验(显着性检验)。当样本含量增大时,样本均数的分布趋向正态,这可看图6.1,t分布曲线以ν=9的一条比ν=3的更近似正态分布,再看附表3,表最下一行ν为∞时的t分布即是正态分布。故u检验用于大样本。
在仅有一条的标准正态曲线上,以u=1.96与-1.96为界,从此处向外的尾部面积共占5%,即∣u∣≥1.96相应的P值为0.05,又∣u∣≥2.58相应的P为0.01。通常我们取α=0.05或α=0.011作为显着性检验水准,故临界值u[XB]0.05[/XB]=1.963及u[XB]0.01[/XB]=2.58最好能记住而省得查表。
一、两均数的比较
例7.6 某工业区卫生防疫站为掌握学龄儿童免疫球蛋白水平,对一批无结核及肾炎病史,一月内无急性感染,又未进行预防接种的学生作了血清IgM(mg/dl)测定,其中12岁男孩73人的X±S为125±54,12岁女孩68人的为153±75,试比较12岁男、女孩的IgM水平有无显着差别。
这里令男生为第1组,女生为第2组。
(1)检验假设H[XB]0[/XB]:μ[XB]1[/XB]=μ[XB]2[/XB];H[XB]1[/XB]:μ[XB]1[/XB]≠μ[XB]2[/XB]。
(2)定α=0.05则对应于P为0.05时的u[XB]0.05[/XB]值为1.96。
(3)求两均数的相差数X[XB]1[/XB]-X[XB]2[/XB]、两均数相差的标准误S[XB]χ1[/XB]-[XB]χ2[/XB]及u值。此外,计算S[XB]χ1[/XB]-[XB]χ2[/XB]的公式为
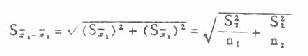 (7.5)
(7.5)
将有关数字代入得
X[XB]1[/XB]-X[XB]2[/XB]=125-153=-28

然后求u
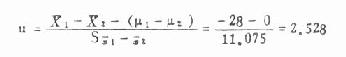
(4)结论 因│u┃>u[XB]0.05[/XB]=1.96,P<0.05。在α=0.05水准处拒绝H[XB]0[/XB]而接受H[XB]1[/XB],即μ[XB]1[/XB]≠μ[XB]2[/XB],故认为12岁女孩的血清免疫球蛋白IgM高于同龄男孩。
二、两个率的比较
关于计数资料,求出特征数百分率后,率与率的比较一般采用第三章介绍的X[SB]2[/SB]检验法,在大样本时,根据样本率分布呈正态分布的特点,也可用u检验。
例7.7 某地曾流行一种原因不明的皮炎,有关部门进行调查时,以宅旁有桑毛虫寄生树的人群为观察组(第1组),以宅旁无该树者为对照组(第2组),两组患病率如下,经显着性检验可得什么结论?
表7.4 两组皮炎患病率
| 组 别 | 观察例数 | 患者 | 患病率(%) |
| 观察组 | 144 | 105 | 72.92 |
| 对照组 | 139 | 66 | 47.48 |
| 合 计 | 283 | 171 | 60.42 |
(1)检验假设 H[XB]O[/XB]:两组相应的总体率相等即π[XB]1[/XB]=π[XB]2[/XB],H[XB]1[/XB]:π[XB]1[/XB]≠π[XB]2[/XB]。
(2)显著性水准 为使结论更加可靠,定α=0.01,则1%界u[XB]0.01[/XB]=2.58。
(3)求两样百分率的相差、两百分率相差的标准误Sp1—p2及u值。
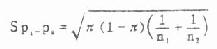
式内π为两组合计百分率,此例为0.6042,见表7.4合计栏。
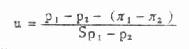 (7.6)
(7.6)
将有关数字代入得

(4)结论 │u│=4.379>u[XB]0.01[/XB]=2.58,P<0.01,也即在α=0.01水准处拒绝H[XB]0[/XB],接受H[XB]1[/XB],即μ[XB]1[/XB]≠μ[XB]2[/XB],宅旁有桑毛虫寄生树的人群皮炎患病率较高。
此外,两百率相差的标准误Sp[XB]1[/XB]-p[XB]2[/XB]还有近似计算公式如下;
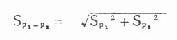 (7.7)
(7.7)
式中S[SB]2[/SB][XB]P1[/XB]、S[SB]5[/SB][XB]P2[/XB]分别为第1、2两组百分比的标准误的平方,标准误计算公式即式(6.4)

用上例数据代入可算得

这里,标准误与u值尽管和前面算得的稍有出入,但还是│u│>u[XB]0.01[/XB]=2.58,P<0.01,结论相同。
