第二节 直线回归
一、直线回归方程的意义
计算出相关系数后,如果r显着,且又需要进一步了解两变量中一个变量依另一个变量而变动的规律时,则可进行回归分析。
“回归”是个借用已久因而相沿成习的名称。若某一变量(Y)随另一变量(X)的变动而变动,则称X为自变量,Y为应变量。这种关系在数学上被称为Y是X的函数,但在医学领域里,自变量与应变量的关系和数学上的函数关系有所不同。例如成年人年龄和血压的关系,通过大量调查,看出平均收缩压随年龄的增长而增高,并且呈直线趋,但各点并非恰好都在直线上。为强调这一区别,统计上称这是血压在年龄上的回归。
直线回归分析的任务就是建立一个描述应变量依自变量而变化的直线方程,并要求各点与该直线纵向距离的平方和为最小。按这个要求计算回归方程的方法称为最小平方法或最小二乘法。所建立的方程是一个二元一次方程式,其标准形式是:
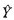 =a+bX(9.5)
=a+bX(9.5)
式(9.4)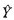 为由X推算得来的Y值,即Y的估计值:a称为截距,它是当X=0时的
为由X推算得来的Y值,即Y的估计值:a称为截距,它是当X=0时的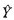 值,即回归直线与纵轴的交点:b称为回归系数,它是回归直线的斜率,其含意是当X每增加一个单位时,
值,即回归直线与纵轴的交点:b称为回归系数,它是回归直线的斜率,其含意是当X每增加一个单位时,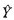 相应增(或减)b个单位。当a与b求得后,直线回归方程就确定了。
相应增(或减)b个单位。当a与b求得后,直线回归方程就确定了。
二、直线回归方程的计算法
仍以表9.1资料为例,根据前面的相关分析以及医学上有关凝血的机理,可知凝血时间依凝血酶浓度而异,且有密切的关系。因此可进一步作由凝血酶浓度(X)推算凝血时间(Y)的回归方程。求直线回归方程的步骤如下:
1.列回归计算表(见表9.1),计算∑X、∑Y、∑X[SB]2[/SB]、∑Y[SB]2[/SB]、∑XY。
2.计算X、Y、∑(X-X)[SB]2[/SB]、∑(X-X)(Y-Y)
X=∑X/n=15.1/15=1.01
Y=∑Y/n=222/15=14.80
∑(X-X)[SB]2[/SB]=∑X[SB]2[/SB]-(∑X)[SB]2[/SB]/n=0.2093
∑(X-X)(Y-Y)=∑XY-∑X·∑Y/n=-1.7800
3.计算回归系数b和截距a。b和a两值计算公式均是根据最小二乘法的原理推算出来的,其公式如下:
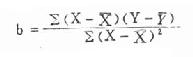 (9.5)
(9.5)
a=Y-bX (9.6)
本例b=-1.7800/0.2093=-8.5045
a=14.80-(-8.5045)(1.01)=23.3895
4.列出回归方程,绘制回归直线,将求得的b和a的值代入到式(9.4),即得所求的回归方程:
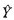 =23.3895-8.504X
=23.3895-8.504X
在凝血酶浓度的实测范围内,即X=0.8到X=1.2之间,任选两个X值(一般选相距较远且直角坐标系上容易读出者),代入此回归方程,即得相应的两个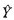 值。例如:
值。例如:
取 X[XB]1[/XB]=0.8,则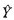 [XB]1[/XB]=23.3895-8.5045×0.8=16.59,
[XB]1[/XB]=23.3895-8.5045×0.8=16.59,
X[XB]2[/XB]=1.2 则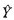 [XB]2[/XB]=23.3895-8.5045×1.2=13.18。
[XB]2[/XB]=23.3895-8.5045×1.2=13.18。
连接(0.8、16.59)和(1.2、13.18)两点所得直线,即为由凝血酶浓度推算凝血时间的回归直线(见图9.9)。须注意回归直线必通过(χ,y )点,并穿过观察点群,直线上下各有一些点散布着,否则计算有误。
三、直线回归方程的假设检验
(一)样本回归系数的假设检验
根据例9.1资料求得的是样本回归系数b,有抽样误差的,需作假设检验,检验其是否是从回归系数为0的假设总体(即β=0)中随机抽得的,也就是检验b与0的差别有无显着性。如果差别有显着性,可认为X与Y间有直线回归存在。
样本回归系数的假设检验亦用t检验。
H[XB]0[/XB]:β=0即Y的变化与X无关;
H[XB]1[/XB]:β≠0。
计算公式为:
 (9.7)
(9.7)
分母S[XB]b[/XB]是样本回归系数b的标准误,计算公式为:
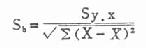 (9.8)
(9.8)
分子Sy.x为各观察值Y距回归线的标准差,即当X的影响被扣去以后Y方面的变异,可按下式计算:
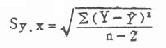 (9.9)
(9.9)
式中∑(Y- 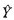 )[SB]2[/SB]为估计误差平方和,常用下式计算:
)[SB]2[/SB]为估计误差平方和,常用下式计算:
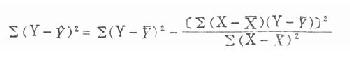 (9.10)
(9.10)
根据数理统计的理论,同一批资料计算所得t[XB]r[/XB]与t[XB]b[/XB]是相同的,即t[XB]r[/XB]=t[XB]b[/XB]。处理资料时可检验相关显著性代替其回归显著性。
由于例9.1资料的r在α=0.01水准上显著,故可判断样本回归系数-8.5045与0的相差有显著性,说明存在凝血时间随凝血酶浓度变化而变化的回归关系。
(二)两样本回归系数相差的假设检验
若有两个可以比较的样本,它们的回归系数分别为b[XB]1[/XB]与b[XB]2[/XB],经检验都为显著,回归系数的标准误分别为S[XB]b1[/XB]和S[XB]b2[/XB]。b[XB]1[/XB]与b[XB]2[/XB]相差的显著性也可用t检验法检验,其计算公式为:
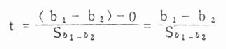 (9.11)
(9.11)
ν=n[XB]1[/XB]+n[XB]2[/XB]-4
式(9.11)中S[XB]b1-b2[/XB]为两样本回归系数之差的标准误,其计算公式为:
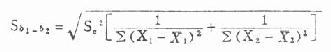 (9.12)
(9.12)
式(9.12)中S[SB]2[/SB][XB]C[/XB]为两样本回归系数的合并方差,其计算公式为:
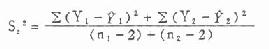 (9.13)
(9.13)
式(9.13)中∑(Y- 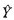 )[SB]2[/SB]为估计误差平方和,即观察值Y与估计值
)[SB]2[/SB]为估计误差平方和,即观察值Y与估计值 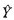 的差数(Y-
的差数(Y- 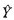 )的平方之和。其计算公式见公式(9.10),
)的平方之和。其计算公式见公式(9.10),
现以实例说明两样本回归系数t检验的步骤。
例9.2 表9.2资料为同一批白蛋白于38℃与25℃条件下,不同时间(分)的凝固百分比,问由此而得的两样本回归系数相差是否显著?
表9.2 白蛋白在两种温度下各不同时间的凝固百分比
| 时间(分) | 凝固百分比(%) | |
| X | Y[XB]1[/XB] | Y[XB]2[/XB] |
| 3 | 7.2 | 12.0 |
| 6 | 18.4 | 30.0 |
| 9 | 30.0 | 44.0 |
| 12 | 40.0 | 53.0 |
| 15 | 49.0 | 66.0 |
| 18 | 58.0 | 81.5 |
| 合计 63 | 202.6 | 286.5 |
本例图示见图9.10,本例计算见图下:
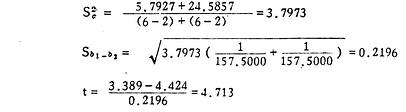
图9.10 白蛋白在两种温度下各不相同时间的凝固百分比
r[XB]1[/XB]=0.998(P<0.01) b[XB]1[/XB]=3.389∑(Y[XB]1[/XB]-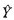 [XB]1[/XB])[SB]2[/SB]=5.7927n[XB]1[/XB]=6
[XB]1[/XB])[SB]2[/SB]=5.7927n[XB]1[/XB]=6
r[XB]2[/XB]=0.996(P<0.01) b[XB]2[/XB]=4.424∑(Y[XB]2[/XB]-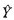 [XB]2[/XB])[SB]2[/SB]=24.5857n[XB]2[/XB]=6
[XB]2[/XB])[SB]2[/SB]=24.5857n[XB]2[/XB]=6
∑(X[XB]1[/XB]-X[XB]1[/XB])[SB]2[/SB]=∑(X[XB]2[/XB]-X[XB]2[/XB])[SB]2[/SB]=157.5000
1.H[XB]0[/XB]:β[XB]1[/XB]-β[XB]2[/XB]=0
H[XB]1[/XB]:β[XB]1[/XB]-β[XB]2[/XB]≠0
α=0.01
2.计算t值:
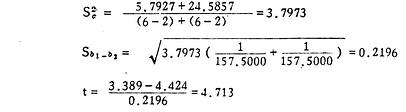
3.查t值表作结论:以ν=6+6-4=8查t值表,得
t[XB]0.01,8[/XB]=2.355,今∣t∣>t[XB]0.01,8[/XB],故P<0.01。
4.判断结果:按α=0.01水准,拒绝H[XB]0[/XB],接受H[XB]1[/XB],故两个回归系数差别显著。说明两条回归直线的斜率不同,两条回归直线中X对Y的影响规律不一致。现b[XB]2[/XB]>b[XB]1[/XB],说明随着时间的增加,蛋白质在38℃时凝固百分比的增加量比在25℃时高。
