第一节 t检验
一、样本均数与总体均数的比较
为了判断观察到的一组计量数据是否与其总体均数接近,两者的相差系同一总体中样本与总体之间的误差,相差不大;还是已超出抽样误差的一般允许范围而存在显着差别?应进行假设检验,下面通过实例介绍t检验的方法步骤。
例7.1 根据大量调查得知,健康成年男子脉搏均数为72次/分,某医生在某山区随机抽查健康成年男子25人,其脉搏均数为74.2次/分,标准差为6.5次/分。根据这个资料能否认为某山区健康成年男子的脉搏数与一般健康成年男子的不同?
在医学领域中有一些公认的生理常数如本例提到的健康成人平均脉搏次数72次/分,一般可看作为总体均数μ。已知在总体均数μ和总体标准差σ已知的情况下可以予测样本均数分布情况,现缺总体标准差,则需用样本标准差来估计它,那么样本均数围绕总体均数散布的情况服从t分布(尤其当样本含量n较小时,)。t分布的基本公式即6.5。
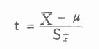
从式中可知,t是样本均数与总体均数之差(以标准误为单位),t的绝对值越大也即X距μ越远。在t分布中距μ越远的样本均数分布得越少(所占百分比小,P值小),后面附表3右上角的示意图中展示了这种关系,如欲知各自由度下t值与其相应的P值可查附表3。
下面回答本例提出的问题而进行假设检验。按一般步骤:
(1)提出检验假设H[XB]0[/XB]与备择假设H[XB]1[/XB]。本例H[XB]0[/XB]为某山区成年男子的脉搏均数与一般成年男子的相等,μ=μ[XB]0[/XB]=72次/分;H[XB]1[/XB]为两者不相等μ≠μ[XB]0[/XB],即μ大于或小于μ[XB]0[/XB](这是双侧检验,如果事先已肯定山区人的脉搏不可能低于一般人,只检验它是否高于一般人,则应用单侧检验,H[XB]1[/XB]必为μ>μ)。
(2)定显著性水准α,并查出临界t值。α是:若检验假设为真但被错误地拒绝的概率。现令α=0.05,本例自由度ν=n-1=25-1=24、查附表3得t[XB]0.05,24[/XB]=2.064。若从观察资料中求出的∣t∣值小于此数,我们就接受H[XB]0[/XB];若等于或大于此值则在α=0.05水准处拒绝H[XB]0[/XB]而接受H[XB]1[/XB]。
(3)求样本均数X、标准差S及标准误S[XB]χ[/XB]并进而算出检验统计量t。现已知X=74.2次/分,S=6.5次/分,只要求出S[XB]χ[/XB]及t值即可。
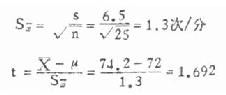
(4)下结论:因∣t∣t[XB]0.05,24[/XB]=2.064,所以检验假设H[XB]0[/XB]得以接受,从而认为就本资料看,尚不能得出山区健康成年人的脉搏数不同于一般人而具有显著差别的结论。
二、成对资料样本均数的比较
上面介绍了已知总体均数时的显着性检验方法,但有时我们并不知道总体均数,且医学数据资料中更为常见的是成对资料,若一批某病病人治疗前有某项测定记录,治疗后再次测定以观察疗效,这样,观察n例就有n对数据,这即是成对资料(也可对动物做成病理模型进行治疗实验以收集类似的成对资料);如果有两种处理要比较,将每一份标本分成两份各接受一种处理,这样观察到的一批数据也是成对资料,医学科研中有时无法对同一批对象进行前后或对应观察,而只得将病人(或实验动物)配成对子,尽量使同对中的两者在性别、年龄或其它可能会影响处理效果的各种条件方面极为相似,然后分别给以一种不同的处理后观察反应,这样获得的许多对不可拆散的数据同样是成对资料。由于成对资料可控制个体差异使之较小,故检验效率是较高的。
关于成对资料,每对数据始终相联这是它的特点,我们可以先初步观察每对数据的差别情况,进一步算出平均相差作为样本均数,再与假设的总体均数比较看相差是否显著,下面举实例说明检验过程。
表 7.1 豚鼠注入上腺素前后每分钟灌流滴数
| 豚鼠号 | 每分钟灌流滴数 | ||
| 用药前 | 用药后 | 增加数d | |
| 1 | 30 | 46 | 16 |
| 2 | 38 | 50 | 12 |
| 3 | 48 | 52 | 4 |
| 4 | 48 | 52 | 4 |
| 5 | 60 | 58 | -2 |
| 6 | 46 | 64 | 18 |
| 7 | 26 | 56 | 30 |
| 8 | 58 | 54 | -4 |
| 9 | 46 | 54 | 8 |
| 10 | 48 | 58 | 10 |
| 11 | 44 | 36 | -8 |
| 12 | 46 | 54 | 8 |
| 总 计 | — | — | 96 |
例7.2 为了验证肾上腺素有无降低呼吸道阻力的作用,以豚鼠12只,进行支气管灌流实验,在注入定量肾上腺素前后,测定每分钟灌流滴数,结果见表7.1,问用药后灌流速度有无显著增加?
(1)假设用药前后灌流滴数相同,则相差的总体均数μ为0;即H[XB]0[/XB]:μ=μ[XB]0[/XB];H[XB]1[/XB]:μ≠μ[XB]0[/XB]。
(2)令显著性水准α=0.05,由本例ν=12-1=11查得临界值t[XB]0.05,11[/XB]=[XB]2.201[/XB]。
(3)求样本统计量平均相差数d、差数的标准差S[XB]d[/XB]、标准误Sd及检验统计量t值。

(4)下结论。今∣t∣t[XB]0.05,11[/XB],p <0.05,故认为检验假设μ=μ[XB]0[/XB]难以接受,在α=0.05水准外拒绝H[XB]O[/XB]而接受H[XB]1[/XB],相差显著,注入肾上腺素后每分钟灌流滴数比注射前要多。
例7.3 从以往资料发现,慢性支气管炎病人血中胆碱酯酶活性常常偏高。某校药理教研室将同性别同年龄的病人与健康人配成8对,测量该值加以比较,资料如下。问可否通过这一资料得出较为明确的结论?
表7.2 慢性气管炎病人与健康人血液胆碱酯酶活性测定(μM/ml)
| 对子序号 | 病人组,X[XB]1[/XB] | 健康人组,X[XB]2[/XB] | 差数 D=X[XB]1[/XB]-X[XB]2[/XB] |
| 1 | 3.28 | 2.36 | 0.92 |
| 2 | 2.60 | 2.40 | 0.20 |
| 3 | 3.32 | 2.40 | 0.92 |
| 4 | 2.72 | 2.52 | 0.20 |
| 5 | 2.38 | 3.04 | -0.66 |
| 6 | 3.64 | 2.64 | 1.00 |
| 7 | 2.98 | 2.56 | 0.42 |
| 8 | 4.40 | 2.40 | 2.00 |
(1)检验假设H[XB]0[/XB]:μ=μ[XB]0[/XB];H[XB]1[/XB]:μ>μ[XB]0[/XB]
(2)令α=0.05,得t[XB]0.05,7[/XB]=1.895(单侧)
(3)用差数求统计量
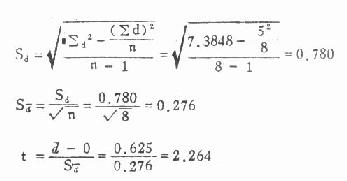
(4)结论∣t∣=2.264>t[XB]0.05,7[/XB]=1.895,P<0.05,在α=0.05水准处拒绝H[XB]0[/XB],接受备择假设,认为慢性气管炎病人血中胆碱酯酶高于正常人。
上例用了单侧检验是因为事先并不认为该类病人血中胆碱酯含量会出现低于健康人的情况。
三、两组资料样本均数的比较
在日常工作中,我们经常要比较某两组计量资料的均数间有无显着差别,如研究不同疗法的降压效果或两种不同制剂对杀灭鼠体内钩虫的效果(条数)等。这时假若事先难以找到年龄、性别等条件完全一样的人(或动物)作配对比较,那么不能求每对的差数只能先算出各组的均数,然后进行比较。两组例数可以相等也可稍有出入。检验的方法同样是先假定两组相应的总体均数相等,看两组均数实际相差与此假设是否靠近,近则把相差看成抽样误差表现,远到一定界限则认为由抽样误差造成这样大的相差的可能性实在太小,拒绝假设而接受H[XB]1[/XB],作出两总体不相等的结论。
例7.4 为观察中成药青黛明矾片对急性黄疸肝炎的退黄效果,以单用输液保肝的病人作为对照进行了观察,两组患者均为成人,黄疸指数在30-50之间,各人退黄天数如下,试比较用药组(1组)与对照组(2组)退黄天数有无显著差别。
表7.3 急性黄疸性肝炎病人的退黄天数
| 中药组,X[XB]1[/XB] | 5 | 10 | 14 | 21 | 17 | ∑X[XB]1[/XB]=67 | |
| 对照组,X[XB]2[/XB] | 18 | 21 | 30 | 23 | 22 | 22 | ∑X[XB]2[/XB]=136 |
(1)检验假设 设该药对缩短退黄天数无效,两组的总体均数相等,即H[XB]0[/XB]=μ[XB]1[/XB]=μ[XB]2[/XB];H[XB]1[/XB]:μ[XB]1[/XB]≠μ[XB]2[/XB]。
(2)求自由度ν
ν=n[XB]1[/XB]+n[XB]2[/XB]-2
=5+6-2=9 (7.1)
定α=0.05,ν=9时的t值为t[XB]0.05,9[/XB]=2.262
(3)计算各组均数,合并方差S[SB]2[/SB][XB]c[/XB]及两均数相差的标准误S[XB]χ1-χ2[/XB],然后求t值。
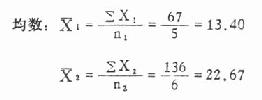
合并方差:  (7.2)
(7.2)
代入得 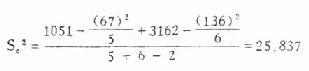
两均数相差的标准误:
 (7.3)
(7.3)
代入得

求t:
 (7.4)
(7.4)
(4)下结论 因│t┃>t[XB]0.05,9[/XB],P<0.02,所以我们在α=0.05水准处拒绝H[XB]0[/XB]而接受H[XB]1[/XB],两者平均退黄天数和有显著差别,服青黛明矾片药的病人退黄天数较短。如果检验假设属实,这样的结论也还可能下错,但概率在2%以下。
上例为两组资料均数间的比较,与前面成对资料的t检验有些区别。前者每对中两数据不能分离,后者任一组中的各数据可以在组内前后互换位置;前者只有一个样本平均差数d对应于一个假设的总体平均差数μ[XB]0[/XB],后者,认为X[XB]1[/XB]为第一个总体的随机样本均数,X[XB]2[/XB]则来自μ[XB]2[/XB],所以后者要计算两组合并的方差S[SB]2[/SB][XB]c[/XB](方差是标准差的平方)。再者,与前者相比标准误、自由度的计算方法也不相同。
例7.5 某人测定半岁至1岁小儿、7至8岁儿童各9人的免疫球蛋白IgG(国际单位/ml),算得平均数与标准差前者(第1组)为55.1± 11.5,后者(第2组)为 95.5 ±17.8,试检验这两种不同年龄的人免疫球蛋白IgG有无显著差别。
(1)检验假设H[XB]0[/XB]:μ[XB]1[/XB]=μ[XB]2[/XB];H[XB]1[/XB]:μ[XB]1[/XB]≠μ[XB]2[/XB]。
(2)令α=0.01,查自由度ν=9+9-2=16时的临界值,得t[XB]0.01,16[/XB]=2.921
(3)求统计量 已知X[XB]1[/XB]=55.1,X[XB]2[/XB]=95.5,至于求t值时作为分母的标准误,在暂缺原始数据时由已知的两个标准差先推算出合并方差S[XB]c[/XB][SB]2[/SB]进而求出S[XB]χ1[/XB]-[XB]χ2[/XB]即可,方法如下;
①一般方法;根据标准差算式
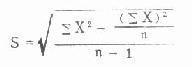
则
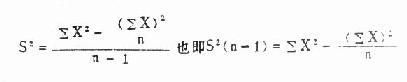
于是
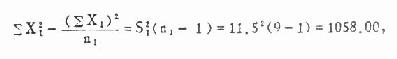
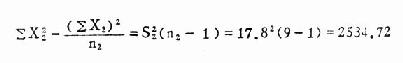
由式(7.2)
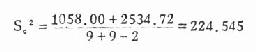
由式(7.3)
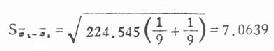
②在两组例数相等时也可直接用S[XB]1[/XB]、S[XB]2[/XB]代入下式求S[XB]χ1[/XB]-[XB]χ2[/XB],结果一样。
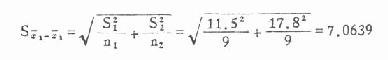
现已有了均数及标准误可由X[XB]1[/XB]、X[XB]2[/XB]、S[XB]χ1[/XB]-[XB]χ2[/XB]求出t值。

(4)结论 │t│>=5.719>t[XB]0.01,16[/XB]=2.921,P<0.001,在α=0.01水准处拒绝H[XB]0[/XB],接受H[XB]1[/XB],两年龄组的人免疫球蛋白IgG的均数相差显著,7-8岁组的高于小几组。
关于检验水准α定在0.05还是0.01或其它处,要看检验者事先对结论的可靠性要求之高低而定。本例定α=0.01,要求是较高的,最后查出P值小于0.001就更说明X[XB]1[/XB]-X[XB]2[/XB]=-40.4随机来自μ[XB]1[/XB]-μ[XB]2[/XB]=0的假设总体的可能性是很小的。
